An up-to-date list is available on Google Scholar.
2023
-
×
![]()
Characterizing Snowpack with 60 GHz FMCW Millimeter-Wave Radar Sensors
Stijn Wielandt, Ivo Marković, Lonnie Chien, Diana Morales, and
3 more authors
In 2023 57th Asilomar Conference on Signals, Systems, and Computers
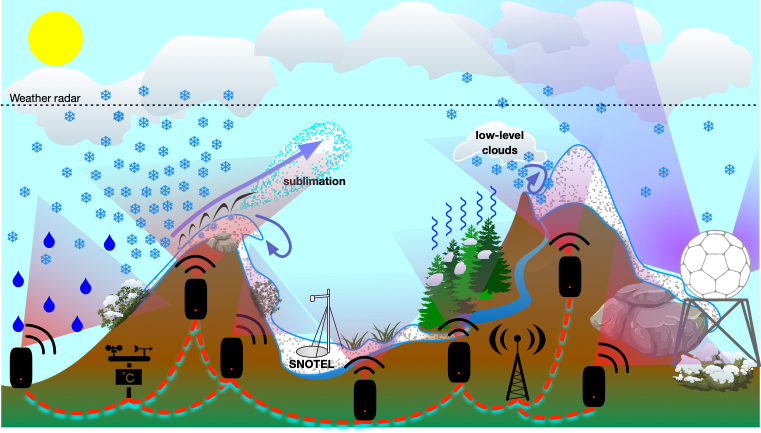
Snowpack is a vital component of Earth’s hydrological cycle and one of the most sensitive to global warming. In order to develop a predictive understanding of the hydrological and biogeochemical dynamics in snow-dominated watersheds, scientists and water resources managers need spatially and tempo- rally dense data sets of snowpack parameters, which could be obtained by networks of low-cost, low-power, distributed sensors. We investigate how 60 GHz frequency modulated continuous wave (FMCW) radar systems-on-chips (SoCs) can be used for measuring a variety of snowpack parameters. For snow depth measurements, we present a dedicated radar detection algorithm that detects the top of the observed snowpack, and we compare its performance to the established cell averaging constant false alarm rate (CA-CFAR) technique. We also evaluate the impact of non-coherent integration of radar frames over receive channels and over time. For measuring snow density and snow water equivalent (SWE), we rely on an adjustment for the signal’s propagation speed in the snowpack based on prior knowledge about the radar’s true distance to the ground. Our lab and field experiments show that snow layers can be detected, bulk snow density can be calculated, and the 90 th percentile of snow depth measurement errors is 25 mm.
2022
-
×
![]()
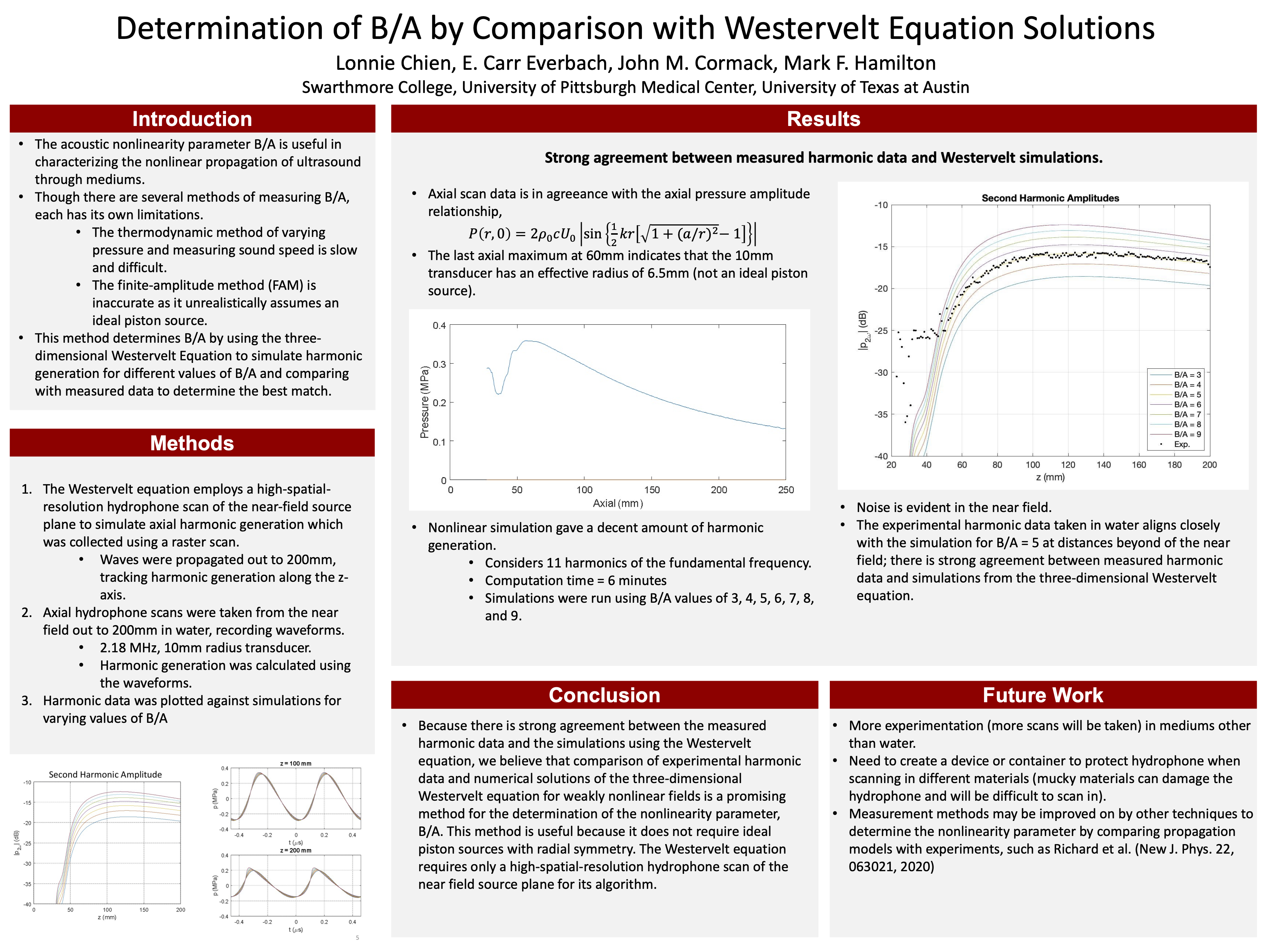
Determination of nonlinearity parameter B/A of liquids by comparison with solutions of the three-dimensional Westervelt equation
Lonnie Chien, John Cormack, E. Carr Everbach, and Mark Hamilton
In Proceedings of Meetings on Acoustics, May 2022
Though nonlinear propagation depends upon the nonlinearity parameter B/A of the medium, it is often difficult to measure accurately. Thermodynamic methods often require high temperature and pressure excursions that can damage fragile molecules. Finite-amplitude methods often require unrealistic assumptions of ideal piston sources to account for diffraction effects. An alternative, described here, is to use the numerical solution of the three-dimensional Westervelt equation for weakly nonlinear fields (considering up to tens of harmonics of the fundamental frequency), and to match measured harmonic generation with that for simulated media. In particular, we follow Jafarzadeh et al. [Ultrasound Med. Biol. 47, 809 (2021)] to find that the nonlinearity parameter of a liquid can be recovered by determining the best match between measurements and simulations of media with different B/A values. Ideal piston sources with radial symmetry are not required, only a high-spatial-resolution hydrophone scan of the near-field source plane. Other techniques to determine the nonlinearity parameter by comparing propagation models with experiments, such as Richard et al. (New J. Phys. 22, 063021, 2020), may improve on earlier measurement methods.